Noktanın Analitiği - 1

Dik koordinat sisteminde

A(k2 + 2, 1 - n) ve B(n - 1, k + n) noktaları aynı bölgededir.

Buna göre,

I. M(k, n) noktası IV. bölgededir.
II. N(k . n, -k) noktası II. bölgededir.
III. P(k + n, k - n) noktası III. bölgededir,

Birim karelere ayrılmış yukarıdaki şekil üzerine dik koordinat sistemi yerleştiriliyor.
Bu durumda A noktasının apsisi -4 ve B noktasının ordinatı -2 oluyor.

Analitik düzlemde,
A(k + 2, k - 1) ve B ( k -2 , k - 4 )

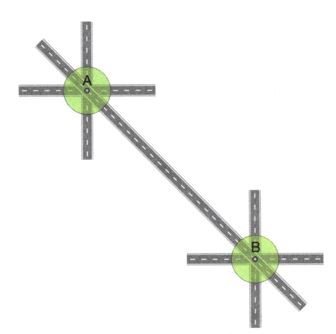
Şekildeki gibi bazı doğrusal karayollarının kesiştiği A ve B yerleşim birimi merkezleri koordinatlar eksenine taşındığında, I. bölgede A(6 - 2k, 2 + 2m) ve II. bölgede
B(2 - k, 6 - 2m) koordinatlarıyla temsil edebilmektedir.

Dik koordinat sistemindeki bir A(k, n) noktasının x eksenine uzaklığı |n| birim, y eksenine uzaklığı |k| birimdir.
Koordinat düzlemindeki bu A noktası A(a - 2, -12) şeklindede ifade edilebilip, bu noktanın x eksenine olan uzaklığı, y eksenine olan uzaklığının 3 katı olmaktadır.

Analitik düzlemde, A(3k + 1, 2k + 9) noktası eksenlere eşit uzaklıktadır.

Analitik düzlemde A(-6, 2) ve B(3, 5) noktaları işaretleniyor. x ve y eksenleri döndürülmeden ötelenerek, koordinat sistemindeki orijin noktası A noktası üzerine getiriliyor.

Koordinat doğrusunda A(- 5), B(x) ve C(2)noktaları gösterilmiştir.

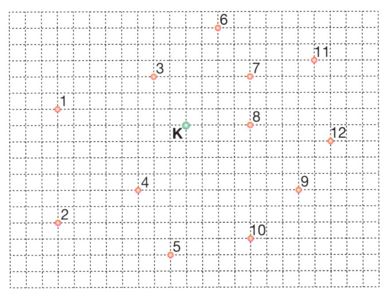
Askeri bir tatbikatın takip edildiği birim karelerden oluşan ekran görüntüsünde, K haricindeki 12 adet nokta düşman hedeflerini göstermektedir.

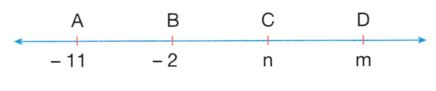
n > 0 olmak üzere, koordinat doğrusunda A(- 8) noktası,B(- 20) noktası ile C(2n) noktaları ortasındadır.

Analitik düzlemde, A(3, t - 4) ve B(-1, t + 2) noktaları veriliyor.

Analitik düzlemde bulunan bir A(2a - 1, 3a + 1) noktasının y ekseni üzerinde olduğu biliniyor.

Buna göre,
B(2a + 3, 3 a - 1 )

ABC ve ACB tümler açılar, DE ± BC A (-2 ,12), B(a, 0), C(16, 0) Salim Bey’in kesip duvara diğer suntalara dayamak için yere bıraktığı ABC biçinindeki parça, analitik
düzlemde modellendiğinde yer düzlemi x eksenini, suntaların DE kenarı da y eksenini temsil etmektedir.

Koordinat doğrusunda A ( - 11), B(- 2), C(n) ve D(m) noktaları gösterilmiştir.

|A C |= A . |B C |
|BC| = 2 . |CD|

Analitik düzlemde, A(a, b) ve B(c, d) noktaları için,
b - d = 4
c - a = 3

Analitik düzlemde, A(3, 7) noktasının C(x, 0) noktasına ve orijine uzaklığı eşittir.

Analitik düzlemde, A(3k - 1, k+ 3) noktasının koordinatları eşittir.

Analitik düzlemde,

I. A(3, 4) ile B(- 1, 2) noktalarının koordinatları toplamı 8 dir.
II. C (- 1, 6) noktasının apsisi ile D(1, 6) noktasının ordinatı toplamı 5 tir.
III. E(- 1,1) noktası dördüncü bölgededir,